Ultracold Atoms Group at the University of Washington

Bose-Einstein Condensate Interferometry

In this project, we are using the high coherence properties of a Bose-Einstein condensate (BEC) to enhance precision atomic interferometry. One specific goal is a high-accuracy measurement of the fine structure constant (α) which in turn tests the fundamental theory of quantum electrodynamics.

Optical Standing Waves as Beamsplitters:

Standing waves of light can coherently manipulate (split or combine) atomic de-Broglie waves of different momentum. Such standing waves can then act as diffraction gratings for atoms and be used as beamsplitters and mirrors for atom interferometry. For stationary atoms (as opposed to atomic beams), the standing wave needs to be pulsed in time, thus realizing time-domain atom interferometry. A review of coherent manipulation of atomic deBroglie waves with standing light waves can be found in [1]. KDpulse

The picture shows the splitting of a Yb Bose-Einstein condensate into multiple momentum states through the action of a pulsed standing wave optical grating. In this case, the standing wave pulse was applied horizontally and the initial 0 momentum state of the atoms evolved (diffracted) into a superposition of multiple momentum states: -2ħk, 0, +2ħk in (a) and from -8ħk to +8ħk in (b). Here k is the wavevector of the (near-resonant) laser light. The few microseconds-long diffraction pulse (low power in (a) and higher power in (b)) was applied immediately after releasing the atoms from the trap and the image was taken after several milliseconds time-of-flight, at which time, the different momentum states had fully separated. This image also gives an indication of the narrow momemtum width of the condensate compared to the momentum of a single photon (compare size of each atom cloud to their separation). This is a key element in our interferometer.

BEC interferometry:

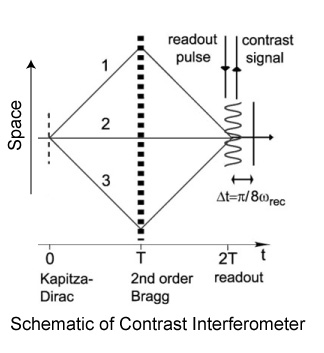
BECs are the most monochromatic source of atoms and can bring to atomic interferometry the same advantages that laser light brings to optical interferometry. The interferometer geometry of choice depends on the measurement of interest. In general, you want to make your interferometer signal sensitive to only the quantity of interest and insensitive (to the extent possible) to other effects. We are currently focussed on a symmetric 3-path geometry where we read out the contrast of the atomic interference pattern as a function of time (see figure). The three paths are separated by multiples of the photon recoil momentum. KDpulse

Measuring α with a BEC interferometer:

The fine structure constant α determines the strength of interaction between light and matter and is the fundamental coupling parameter in quantum electrodynamics (QED). The best determination of α comes from a highly accurate measurement of the electron magnetic moment in conjunction with a sophisticated QED calculation [2]. A route to α that does not involve complex QED calculations thus also sensitively tests the fundamental light-matter interaction theory. Such a route is available through a combination of precision measurements in atomic physics, with the current limiting factor being the photon recoil frequency measurement of a test particle. The recoil frequency corresponds to the kinetic energy of a particle (initially at rest) after it has absorbed a photon. We choose Yb as our test particle and measure the recoil frequency by atom interferometry. Earlier work demonstrating this technique using a sodium atom BEC can be found in [3].

Our Yb BEC contrast Interferometer:

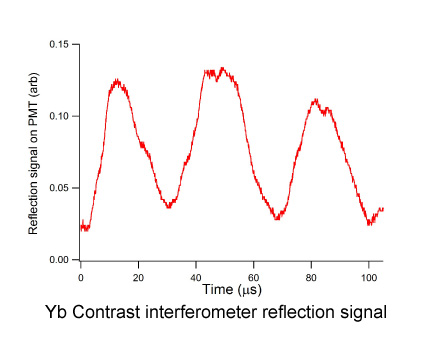
The recoil frequency of Yb atoms is measured by BEC interferometry in our experiment. readout

The phase accrued by paths 1 and 3 are multiples of the recoil frequency and are measured against the phase of the "stationary" path 2. The symmetric 3-path geometry of our design (see schematic - diffraction and readout pulses are along the vertical axis in the figure) suppresses effects from vibrations, rotations, and accelerations. Our choice of atom makes the measurement also insensitive to ambient magnetic fields, since Yb has zero magnetic moment in its ground state. Additionally Yb has several isotopes allowing for systematic checks within the same apparatus. Shown on the right is one of the first reflection signals generated by our Yb contrast interferometer. The oscillation period is 34μs, corresponding to eight times the recoil frequency. The central phase can be determined to about 10mrad. This determines the recoil frequency to about 30ppm (T=1.7ms in this case) in a single experimental iteration. We plan to increase the precision by increasing T (factor of 3), using atomic states (paths 1 and 3) of higher momentum (factor of 20), and averaging over several experimental iterations. A sub part-per-billion precision is feasible in this experiment.
An important consideration in atom interferometry is the role of interactions between particles (absent in optical interferometers). Our recent analysis relevant to BEC interferometers can be found in [4].
Our experiment is also suitable for the comparison of Bose vs Fermi interferometers (Yb has both kinds of isotopes), and basic studies in decoherence and measurement back-action.

This project is supported by the National Science Foundation and by the National Institute of Standards and Techonology.

References:
[1] S. Gupta, A.E. Leanhardt, A.D. Cronin, and D.E. Pritchard, Coherent manipulation of atoms with standing light waves, C.R. Acad. Sci. IV-Phys. 2, 479 (2001).
[2] D. Hanneke, S. Fogwell, and G. Gabrielse, New measurement of the electron magnetic moment and the fine structure constant, Phys. Rev. Lett. 100, 120801 (2008).
[3] S. Gupta, K. Dieckmann, Z. Hadzibabic, and D.E. Pritchard, Contrast Interferometry using Bose-Einstein condensates to Measure h/m and α, Phys. Rev. Lett. 89, 140401 (2002).
[4] A.O. Jamison, J.N. Kutz, and S. Gupta, Atomic Interactions in Precision Interferometry Using Bose-Einstein Condensates, Phys. Rev. A. 84, 043643 (2011).